Significant Figures:
|
Learning Targets:
Students will be able to...
|
READ: Purpose & Measurements
Significant Figures (Sig Figs) are the number of digits used to express a measurement or calculation. Sig Figs are used to show the precision of a measurement or calculation. The more sig figs used, the more precise a measurement or calculation. Sig figs are also used to determine the rules for rounding the final answers to numerical calculations.
Significant Figures (Sig Figs) are the number of digits used to express a measurement or calculation. Sig Figs are used to show the precision of a measurement or calculation. The more sig figs used, the more precise a measurement or calculation. Sig figs are also used to determine the rules for rounding the final answers to numerical calculations.
|
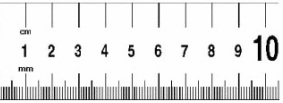
The top of this ruler is only precise to the nearest 1 cm while the bottom of the ruler is precise to the nearest 0.1 cm. The digital scales pictured also have different levels of precision (displaying measurements to the nearest 0.01 gram and 0.1 gram). Greater precision in tools can provide more Sig Figs in measurements.
|
The Rules for Identifying and Counting Sig Figs in Numbers
1. Non-zero digits (1-9) are ALWAYS significant. Always. Forever.
Examples: 1859 has four sig figs. 924 has three sig figs.
2. Zeros between other digits are significant. These are “middle zeros.”
Examples: 406 has three sig figs. 10,045 has five sig figs.
3. Zeros that show precision of measurement are significant. These are "trailing zeros."
Example: 4.10 and .350 each have three sig figs.
Basically....any digit that was actually measured is considered to be significant. But what about numbers that are rounded?
1. Non-zero digits (1-9) are ALWAYS significant. Always. Forever.
Examples: 1859 has four sig figs. 924 has three sig figs.
2. Zeros between other digits are significant. These are “middle zeros.”
Examples: 406 has three sig figs. 10,045 has five sig figs.
3. Zeros that show precision of measurement are significant. These are "trailing zeros."
Example: 4.10 and .350 each have three sig figs.
Basically....any digit that was actually measured is considered to be significant. But what about numbers that are rounded?
|
4. Zeros that are only used to indicate the decimal point are not significant. These are “placeholder zeros" and scientific notation could be used to re-write the number without any zeroes.
Examples: 0.004 and 400 each have one sig fig. 12,000 and 0.00097 each have two sig figs. Understanding these rules is tough -- watch this video! Practice 1: (answers at the bottom of this page) How many sig figs are in these numbers? a. 53 b. 257.4 c. 801.9 d. 0.002345 e. 317.600 f. 300 g. 0.006 h. 77.020 |
|
Calculations with Sig Figs: Multiplying & Dividing
1. Perform the entire calculation without rounding along the way. 2. Round the final answer to have the same number of sig figs as the least of all the numbers used in the calculation. Example: 2.5 × 2.01 × 2.755 = 13.843875 Final Answer = 14 (rounded to 2 sig figs since that was the least number of sig figs of all the factors) Example: 5.375 ÷ 0.012500 = 430 Final Answer = 430.0 (includes 4 sig figs since that was the least number of sig figs in the calculation) Practice 2: (answers at the bottom of this page) a. 3.54 × 0.0082 b. 153 × 0.3 c. 45.605 × 12.2 d. 3845 ÷ 12 e. 16,342 ÷ 18.5 |
Video: Calculating with Sig Figs (multiplication)
|
|
Calculations with Sig Figs: Adding & Subtracting
1. Perform the addition or subtraction without rounding along the way. 2. Round the final answer to the same precision as the least-precise number present in the problem (look at the place value of the numbers: 0.153 is precise to the nearest thousandth while 1.16 is less precise because it is only measured to the nearest hundredth). Example: 0.153 + 1.16 = 1.313 Final Answer = 1.31 (rounded to the hundredths place because that was the precision in the least precise number) Example: 13 - 0.3 = 12.7 Final Answer = 13 (rounded to the ones place because that was the precision in the least precise number.) ***Notice -- only the place value of sig figs matters, the number of sig figs is NOT counted when Adding and Subtracting! Practice 3: (answers at the bottom of this page) a. 34.25 + 17.5 b. 4.034 + 0.27 c. 21.3 - 8.23 d. 138.7 - 1 e. 2558 - 140 |
Video: Calculating with Sig Figs (addition)
|
WATCH: Significant Figures Videos
PRACTICE: Significant Figures
Try this online practice quiz to test your understanding: Practice Quiz
Try this online practice quiz to test your understanding: Practice Quiz
Discussion Questions
- Measuring tools with greater precision generally cost much more than average tools. Describe two professions where precise tools for measuring are vital. Explain your reasoning.
- Sometimes, an estimation is suitable when measuring and reporting numbers. Describe two situations where rounding to the nearest 100 is acceptable. Explain your reasoning.
- People sometimes say, "It's as easy as 2 + 2." However, when rounded to one sig fig, the number 2 could actually be anywhere between 1.50 and 2.49. Show two times when 2 + 2 doesn't equal 4 (when rounded to one sig fig).
- Do some research: how many significant figures are in pi? List another number with the same amount of sig figs.
- Do some research: what is an "exact" number and how many sig figs does it have? List four examples of exact numbers.
|
Answers to Practice 1:
a. 2 b. 4 c. 4 d. 4 e. 6 f. 1 g. 1 h. 5 |
Answers to Practice 2:
a. 0.029 b. 50 c. 556 d. 320 e. 883 |
Answers to Practice 3:
a. 51.8 b. 4.30 c. 13.1 d. 138 e. 2420 |